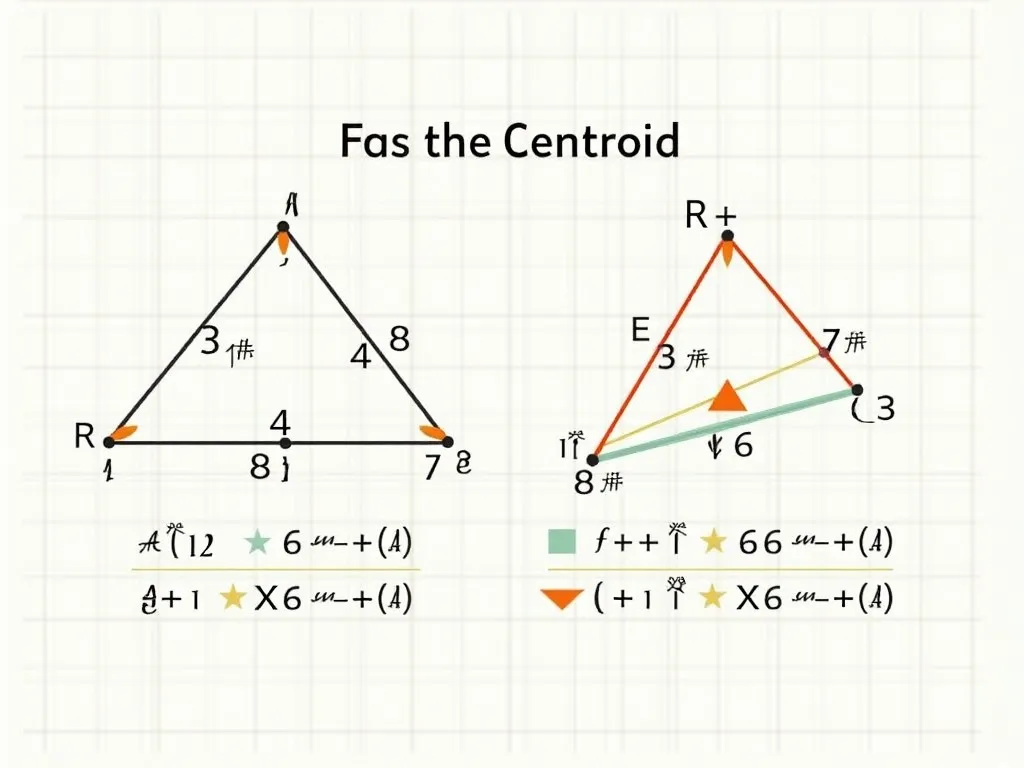
三角形の重心(重心)は、三角形の中線が交わる点です。このページでは、重心の位置を求める方法について詳しく解説します。🟡
三角形の重心とは、各頂点から対辺の中点を結ぶときに、その線分の交点が形成される点です。これを中線と呼びます。
「重心は、物体が完全にバランスを取るための秘密の場所です。」
三角形の頂点をA(x_1, y_1), B(x_2, y_2), C(x_3, y_3)とした場合、重心の座標は以下の公式で求めることができます。
例えば、頂点がA(0, 0), B(6, 0), C(3, 6)の三角形を考えてみましょう。
重心の座標は:
$$ G\left( \frac{0 + 6 + 3}{3}, \frac{0 + 0 + 6}{3} \right) = G\left( 3, 2 \right) $$重心が中線の交点であることの証明には、以下のステップが含まれます:
重心を求める他の方法としては、以下のようなものがあります。
三角形の重心を求めることは、数学の根本的な概念を理解する上で重要です。🎓
重心の求め方を知ることで、より深い数学的な理解を得ることができます。