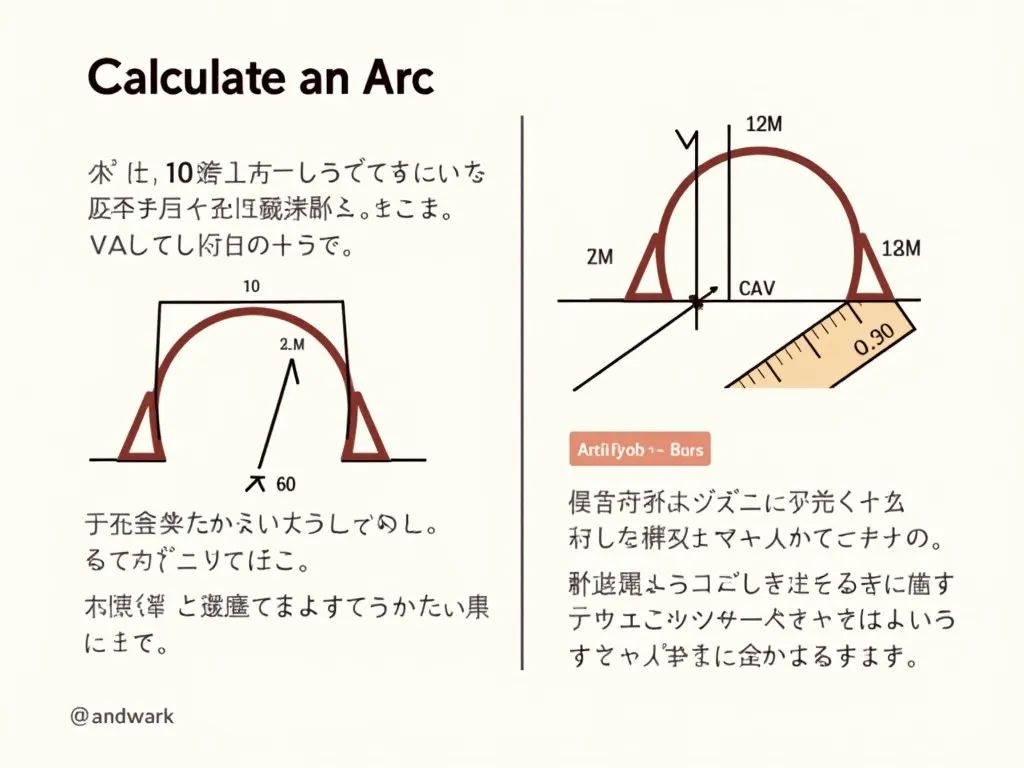
弧とは、円周の一部分であり、弧の長さを求める方法はとても簡単です。一般的に使用される公式は以下の通りです: 弧の長さ \( L = \frac{\theta}{360^\circ} \times 2\pi r \) ここで、\( \theta \)は中心角、\( r \)は円の半径です。
弧の長さを求めるには、まず円周の全長を計算する必要があります。円周の公式は次の通りです:
C = 2\pi r
ここで、円周 \( C \) は円の周囲の長さ、\( r \)は半径です。中心角 \( \theta \) が与えられた場合、弧の長さは円周に対する中心角の割合を使って求められます。
半径が10cm、中心角が60度の扇形を考えてみましょう。弧の長さは次のように計算できます:
\[ L = \frac{60}{360} \times 2\pi \times 10 = \frac{1}{6} \times 2 \times 3.14 \times 10 \approx 10.47\, \text{cm} \]
「この計算方法を知っていると、数学のテストで自信を持てますよ!」✨
弧の長さを求める際には、面積も考慮することが重要です。弧によって形成される扇形の面積は次の公式で求められます:
A = \frac{\theta}{360^\circ} \times \pi r^2
この公式を使って、中心角から面積を求めることができます。
弧の長さを求める際には、中心角と半径が必要です。この公式を覚えておくと、数学の問題を解くのがとても簡単になります。是非、実際の問題でも試してみてください!