こんにちは!今日は「断面係数求め方」について、徹底的に解説していきます。断面係数は、構造力学や材料力学において非常に重要な概念です。💡
断面係数(ざんめんけいすう、Section Modulus)は、部材の曲げ強さを示す指標です。通常、以下の式で表されます:
断面係数が大きければ大きいほど、部材は強い!💪
断面係数と断面二次モーメントは、しばしば混同されますが、それぞれ異なる性質です。断面二次モーメントは部材の断面形状による抵抗力を示しますが、断面係数は曲げに対する強さを表します。
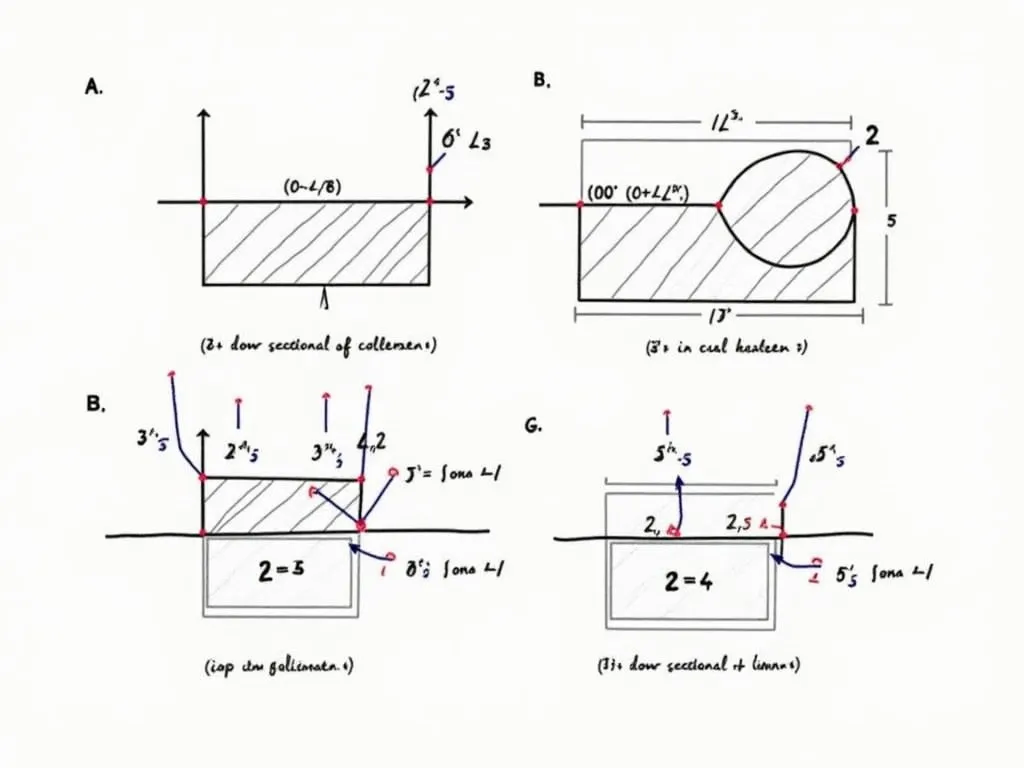
断面係数を求めるためには、部材の断面の形状に応じた公式を利用します。以下は主な断面形状の求め方です:
長方形の断面係数は次のように求められます:
円形の断面係数は以下の式で求められます:
断面係数を計算する際には、以下のポイントに注意しましょう:
これらのポイントを守れば、計算は簡単!😉
断面係数は構造物の耐久性を評価する上で非常に重要な指標です。「断面係数求め方」を理解することで、より良い設計が可能になります。是非この知識を活用してください!
質問やコメントがあれば、どうぞお気軽にお寄せください!